Neuronio artificial
Já no começo do século XX Alan Turing e John Von Newman(MCCULLOCH; PITTS,1943) asseguraram que a inteligência podia ser representada por matemática booleana. Segundo MCCULLOCH&PITTS (1943) este modelo de neurônio é formado por um conjunto de entradas (X0, X1, …, Xn) e as sinapses são representadas por pesos numéricos(wj0, wj1, …, wjn), que podem tanto assumir valor positivo quanto negativo, fazendo com que o neurônio seja excitado ou inibido. Após a multiplicação das entradas pelos pesos,esses resultantes são somados pelo somador (Σ) ou combinador linear e o valor é submetido a uma função de ativação ou função de transferência (T), que gera uma saída.
Neurônios artificiais são estruturas compostas de Entradas, Pesos, Somador, Bias, Função de ativação e Saída.
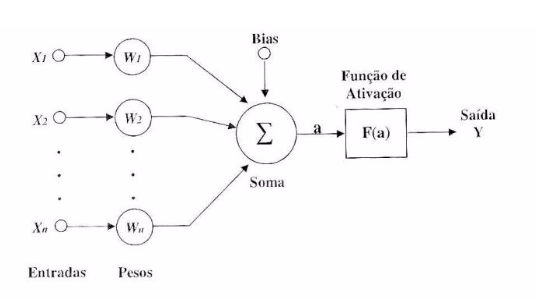
Matematicamente o combinador linear (Σ) deste neurônio (uk) da é representado pela equação:
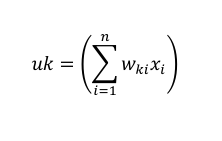
A função de ativação F(a) serve como um limitador da saída restringindo os valores para intervalos previamente definidos. Além de agir sobre os valores de saída do neurônio, a função de ativação também tem a função de aumentar ou diminuir a entrada liquida de um neurônio, tendo geralmente um valor fixo iguala 1 ou -1. Dessa forma, a representação do valor de saída do neurônio seria dada por
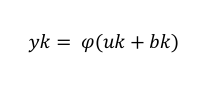
A função de ativação ou função de transferência determina o momento em que o neurônio será ativado, com base no valor que é recebido do somador. Existem diversas funções de ativação, que podem ser binárias ou com uma saída mais abrangente (LISA, 2005) como:
- Função degrau
- Função linear
- Função logística
- Função tangente hiperbólica
Referências
- LISA, Sammer.Merkmalbasierte Zeichenerkennung mittels neuronaler Netze.2005. 124 f. Tese (Doutorado) -Curso de Matemática, Universitat Bayreuth Mathematisches Institut, Bayreuth, 2005. Disponível em: <http://num.math.uni-bayreuth.de/de/thesis/2005/Sammer_Lisa/Sammer_Lisa.pdf>. Acesso em: 29 jun. 2015.
- MCCULLOCH, Warren; PITTS, Walter.A Logical Calculus of the Ideas Immanent in Nervous Activity.1943. Disponível em: http://www.cse.chalmers.se/~coquand/AUTOMATA/mcp.pdf. Acesso em: 14/06/2015